Spin-dependent effects in helical molecular systems, leading to the so-called chirality-induced spin selectivity (CISS) effect, have strongly attracted the attention of the chemical and physical community over the past few years. A large amount of experimental material has been collected so far, and different theoretical approaches have been presented to rationalize the CISS effect. The problem is, however, still a subject of debate. We present a semianalytical coarse-grained atomistic description of the electronic structure of a simple helical molecule, including spin-orbit interactions. For reference, we consider helicene, which is a pure carbon-based helical system with no chiral centers, and which has been previously shown experimentally to display a CISS effect. Our model exploits perturbation theory and a Lowdin-like partitioning to obtain an effective Hamiltonian, where all coupling coefficients depend on the helical geometry and predefined Slater-Koster parameters. As a result, they can be explicitly computed, thus providing physically meaningful orders of magnitude. We further discuss the conditions under which a nonvanishing spin polarization can be obtained in the model. We expect that our approach will serve to bridge the gap between purely phenomenological model Hamiltonians and more advanced first-principles methodologies.
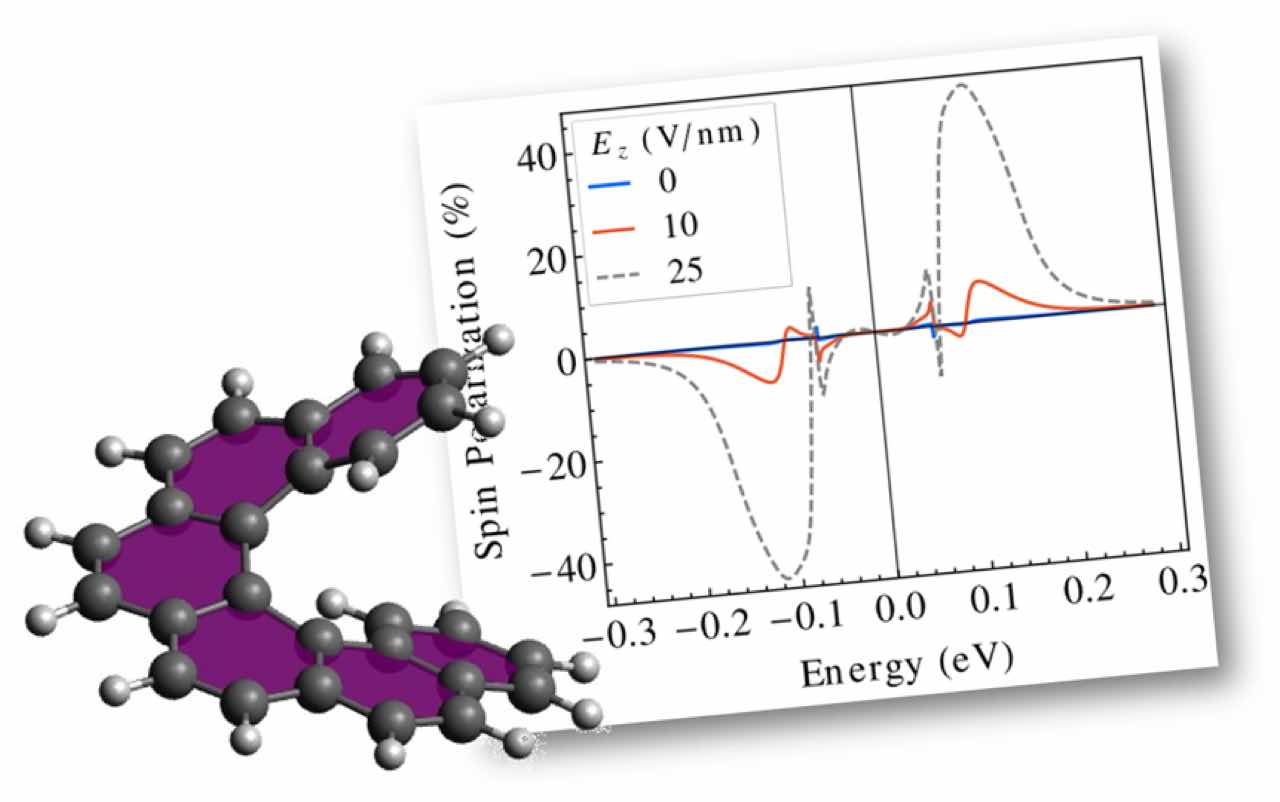
Spin-dependent effects in helical molecular systems, leading to the so-called chirality-induced spin selectivity (CISS) effect, have strongly attracted the attention of the chemical and physical community over the past few years. A large amount of experimental material has been collected so far, and different theoretical approaches have been presented to rationalize the CISS effect. The problem is, however, still a subject of debate. We present a semianalytical coarse-grained atomistic description of the electronic structure of a simple helical molecule, including spin-orbit interactions. For reference, we consider helicene, which is a pure carbon-based helical system with no chiral centers, and which has been previously shown experimentally to display a CISS effect. Our model exploits perturbation theory and a Lowdin-like partitioning to obtain an effective Hamiltonian, where all coupling coefficients depend on the helical geometry and predefined Slater-Koster parameters. As a result, they can be explicitly computed, thus providing physically meaningful orders of magnitude. We further discuss the conditions under which a nonvanishing spin polarization can be obtained in the model. We expect that our approach will serve to bridge the gap between purely phenomenological model Hamiltonians and more advanced first-principles methodologies.
